Pre-Calculus Topics: August 2013

General Information

General information:
YOU MUST KNOW THIS STUFF:

I am in my Math Dept. Office from 12:00 until class on Mon., Wed., and Friday.
Please stop in for help! - I am more than glad to:
- Re-teach a topic OR - Help on a homework problem
- Help with a Math technique that I may have assumed that you knew before entering the class
- We can do more example problems from a topic that seems to be troubling you
****************3rd EXAM - TEST on FRIDAY, NOV. 8th******************
Possible Questions:

Find the RADIAN measure of the angle with the given degree measure.
36 degrees
72 degrees
900 degrees
1200 degrees
-120 degrees
-225 degrees

Find the DEGREE measure of the angle with the given radian measure.
4pi/5
3pi/4
13pi/6
13pi/12

The measure of an angle in standard position is given in DEGREES.
Find the coterminal angle with the given condition.

GIVEN: (-120 degrees) -> Find a coterminal partner between zero and 360 degrees. ____________
GIVEN: (-150 degrees) -> Find a coterminal partner between zero and 360 degrees. ____________
GIVEN: (780 degrees) -> Find a coterminal partner between zero and 360 degrees. ____________
GIVEN: (650 degrees) -> Find a coterminal partner between zero and 360 degrees. ____________

Find an angle between 0 and 2pi RADIANS that is coterminal with:
7pi/3
15pi/4
-13pi/4
-9pi/4

Find the length of an arc that subtends a central angle of 30 degrees
in a circle of radius 8 meters.

Find the length of an arc that subtends a central angle of 3pi/2 radians
in a circle of radius 8 meters.

Find the area of a sector that is formed in a circle of diameter 14 meters.
This sector subtends a central angle of 120 degrees.

Find the area of a sector that is formed in a circle of diameter 14 meters.
This sector subtends a central angle of pi/4 radians.

**********PLUS some from the last double quiz*******************

1) If $7896 is invested at 6%. The interest is compounded monthly.
How much money will be available after 7 years?
2) What is the PRESENT VALUE of $8976 under the conditions that
the money would be invested at 8% for 11 years and compounded daily?
(In other words: What would I need to invest at 8% now to have $8976 in 11 years?)
3) Starting with 2500 units of substance, find the amount remaining after
8 years with continuous compounding under a decomposition of 4%
4) Find the Annual Percentage Yield for 8% compounded continuously.
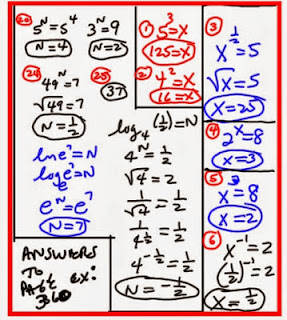
5) Switch each Logarithmic Form to the corresponding Exponential Form.

6) Switch each Exponential Form. to the corresponding Logarithmic Form.
7) Find the value of "z" in each equation

***********Find the Final Amount or Find the Initial Amount
another name for this finding the PRESENT VALUE***************
1) $7000 - at 4% - compounded yearly - for years - results in $8516.570317
2) $7000 - at 4% - compounded monthly - for 5 years - results in $8546.976158
3) $7000 - at 4% - compounded daily - for 5 years - results in $8549.72561
4) $3658 - @ 5% - compounded daily - for 7 years - becomes $5190.824665
5) $3658 - @ 5% - compounded monthly - for 7 years - becomes $5187.175879
6) $3658 - @ 5% - compounded yearly - for 7 years - becomes $5147.17334
7) $8,187.39725 - at 4% - compounded daily - for 5 years - results in $10,000
8) $4,493.4866 - at 4% - compounded daily - for 20 years - results in $10,000
*** With Continuous Compounding any of the four variables can be found given the other 3
**(e = 2.71828182...)*****
9) $3658 - @ 5% - compounded continuously - for 7 years - becomes $5190.949093
10) 9876 - Decaying continuously - @ 6% - for 10 years - becomes 5420.063718
11) $7000 - at 4% - compounded Continuously - for 5 years - results in $8549.819307
12) $8187.307531 - at 4% - compounded Continuously - for 5 years - results in $10,000
13) $4493.289641 - at 4% - compounded Continuously - for 20 years - results in $10,000

A Function is ... (3.1)

A DIFFERENCE QUOTIENT EXAMPLE:

A FUNCTION is...
a "RULE" that explains what mathematical operations will be APPLIED to:
- an INPUT (an "X") to produce the OUTPUT (the "Y" value)
- "X" (the INDEPENDENT VARIABLE)
- a NUMBER from the DOMAIN
- to get the VALUE for Y (the DEPENDENT VARIABLE) from a given "X" VALUE

the DOMAIN is the set of possible "X" values
the RANGE is the set of "Y" values
use letters like "f" or "g" or "h" ... to represent a function

f can also be thought of as a MAPPING (Arrow diagram)
showing how (CONNECTS) each
value from the DOMAIN is
matched to a PARTNER in the RANGE

f can also be pictured as a MACHINE that takes
a given INPUT and produce a SINGLE OUTPUT
using a UNIQUE RULE
"x" is an INPUT and
"y" or "f(x)" is the OUTPUT value

f(x) is read as
- f of x
- f operating on x
- f evaluated at x
- the value of f at x
- the image of x under f

An employee for ACME INDUSTRY earns $9 for each hour worked.
To calculate the EARNINGS for a certain individual we
"Multiply the NUMBER OF HOURS (x) by 9"
g(x) = 9 times x
g(x) = 9x
suppose the DOMAIN is {20,30,40}
then the RANGE will be {180, 270, 360}
g(20) = 9(20) = 180
etc.

If ACME INDUSTRY changes the pay rate to $360 for any
employee that works less than or equal to 40 hours in a given week.
When an employee works more than 40 hours they receive an
additional $10 for each hour over 40. This creates the need for a
special type of function called a PIECEWISE DEFINED FUNCTION.
Two different rules are needed. One rule for less than or equal to 40 hours
and a second rule for over 40 hours.

g(x) = 360 ..................... if 0< x <= 40
g(x) = 360 + 10(x-40) .... if 40 < x

REPRESENTING A FUNCTION:
1) VERBALLY (using words)
2) ALGEBRAICALLY (using a formula ... f(x) = 9x )
3) VISUALLY (use a GRAPH)
4) NUMERICALLY (by use of TABLE)

Function Graphing (3.2)

***************************************************

**************************************************

Information from a Graph (3.3)

Information from a Graph (3.3)

HW for Section 3.3
#5, 7, 19, 21, 31, 33, 47

Topics for this section:
GIVEN A GRAPH:
1) Find the y value for a given x
2) Find the x value(s) for a certain y
3) On what intervals does the graph INCREASE?
4) On what intervals does the graph DECREASE?
5) Are there any RELATIVE MAXIMUMS?
Where do they occur? (x value)?
What are the VALUES THERE (y value)?

A Function's Average Rate of Change (3.4)

example:

**************************************************

September, 2013 - National Geographic Magazine
RISING SEAS

A Graph from the National Oceanic and Atmospheric Administration shows:

The notes below are for
the slope of LINES.

HW for Section 3.4
Page 219 #5,7,9,11,13,15, 21,29

Transforming Functions (3.5)

Transforming Functions (3.5)

answers to first quiz

**********************************************

SECTION NOTES

**************************************************************

Functions can be combined (3.6)

Inverse Functions and 1 to 1 (3.7)

Inverse Functions and 1 to 1 (3.7)

Steps:
1) Turn into algebra Y = ...
2) Switch the x and y
3) now solve for y
(Y must equal a unique value - be a function itself)
4) this y is the INVERSE FUNCTION.
5) now you can put the INV. into words if needed

All functions have the property where each x has one y-partner.
(Graphically: It passes the "VERTICAL LINE TEST".)
If a certain function also has each y with only one x-partner
(Thus, passing a "HORIZONTAL LINE TEST"), it has an INVERSE!

Prefixes like INV or ARC are sometimes used to denote inverse.
Another form looks like f to the -1 power(Not to be confused with RECIPROCAL).

You might say that the INVERSE
undoes what the orginal function did!

To find the inverse of a function f(x)
switch x and y and THEN solve for y.

f(x) = x cubed
switch
x = y cubed
solving for y
y = cube root of x
y = x raised to 1/3 power

(We had to invent the symbols for cube root and 1/3 power.)
The graph of the inverse of f(x) we can graph f(x) and then
rotate this graph through y = x (thus, switching x and y)

A look at Quadratic Functions (4.1)

A look at Quadratic Functions (4.1)

Given the Quadratic Function:.......
"Does Not Exist- DNE" is a possible answer to:

1) Express in STANDARD FORM
2) What (?,?) is the VERTEX?
3) What, if any, is the Maximum value of the function?
4) What, if any, is the Minimum value of the function?
5) Find the x-intercepts
6) Find the y-intercepts
7) What, if any, are the ZEROS?
8) Sketch the graph

BELOW are more notes that I have used
in other courses. Look, if you wish!

Sunday, August 18, 2013